GALERIE     EN COURS     SCENES     MACROS     GUIDE     PORTFOLIO     A PROPOS


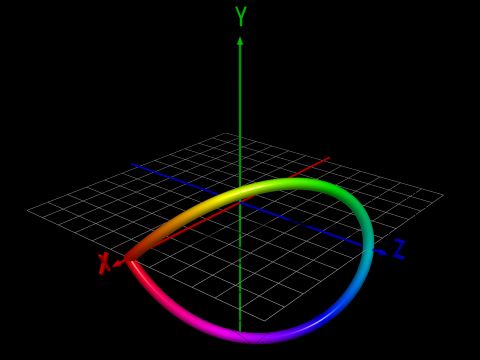
Viviani
C’est un cas particulier d’hippopède de d'Eudoxe vu précédemment. Cette famille de courbes est définie par l'équation paramétrique suivante :
$$\begin{align} x &= a(1+cos(t))\\y &= asin(t)\\z &= 2asin(t/2)\\\\t &\in 0\;..\;2\pi\end{align}$$


Script :

#declare deuxpi = 2*pi;
#declare r = 0.20;

#declare currentPt = <0.00, 0.00, 0.00>;
#declare previousPt = <0.00, 0.00, 0.00>;
#declare theColor = rgb <0.00, 0.00, 0.00>;

#declare a = 3;

#declare i=0;
#declare step=pi/250;
#while (i < deuxpi)
  #set theColor = rgb CH2RGB(degrees(i));
  #set currentPt = a*<1+cos(i), sin(i), 2*sin(i*0.50)>;
  sphere {
    currentPt, r
    pigment { theColor }
    finish { courbeFinish }
    }
  #if(i!=0)
    cylinder {
      previousPt, currentPt, r
      pigment { theColor }
      finish { courbeFinish }
      }
  #end
  #set previousPt = currentPt;
  #set i = i + step;
#end
-- Mêmes remarques que les courbes précédentes.



On obtient alors l'image suivante :
Viviani