Surface 3D à l'ancienne
A l'époque ou les micro-processuer étaient poussifs, la représentation en trois dimensions des surfaces définies par des équations ne se faisait pas avec des sommets, des arêtes et des faces organisés en triangles (mesh), mais avec un rendu "fil de fer". Cette méthode relie les sommets caractéristiques d'un objet avec des droites. En utilisant ce type de rendu, on peut apercevoir l'intérieur de l'objet et les arêtes cachées. Ce type de rendu est trés rapide et ne manque pas d'un certain charme.L'objet est dessiné de cette manière :
object {
surface
pigment {
gradient y
color_map { TheColorMap }
}
finish { specular 1 }
}
Rien de bien compliqué. Un dégradé de couleur suivant l'axe y est utilisé pour colorier les fils.L'objet "surface" est simplement une union{} de tous les points calculés et des lignes qui relient ces points. Un tableau à deux dimensions contient l'ensemble de ces points. Ici PointsArray[][]. Chaque élément du tableau est un point et contient le triplet <x, y, z>.
Le maillage est obtenu en reliant ces points, les sphere{}, avec des droites, les cylinder{}.
Le code ci-dessous est une manière de faire.
#declare surface = union {
#declare xIndex=0;
#while( xIndex < xPts)
#declare zIndex=0;
#while(zIndex < zPts)
#if ( xIndex = 0 )
sphere {
PointsArray[xIndex][zIndex], curveFil
}
#else
cylinder {
PointsArray[xIndex][zIndex],
PointsArray[xIndex-1][zIndex],
curveFil
}
#end
#if (zIndex=0)
sphere {
PointsArray[xIndex][zIndex],
curveFil
}
#else
cylinder {
PointsArray[xIndex][zIndex],
PointsArray[xIndex][zIndex-1],
curveFil
}
#end
#declare zIndex = zIndex + 1;
#end
#declare xIndex = xIndex + 1;
#end
}
Dans notre cas, les surfaces étant définies par des équations, une macro est utilisée pour calculer la valeur de la fonction y = f(x,z).
#macro func (xx,zz) sin(sqrt(xx*xx+zz*zz)) #endOn passe les valeurs xx et zz à la macro qui calcule et renvoi le résultat de la fonction : yy
Et maintenant quelques images ...
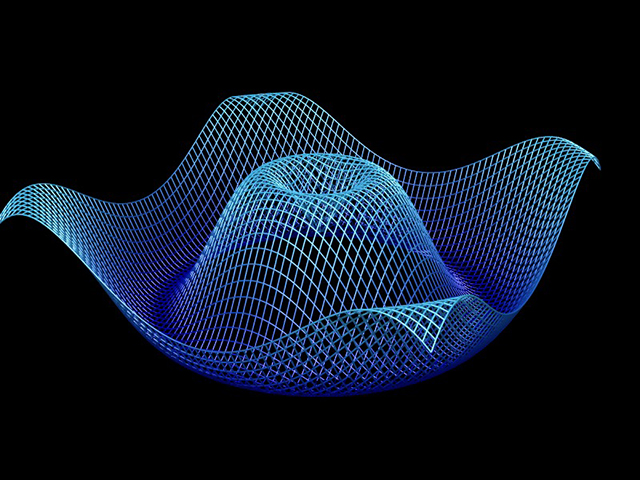 $$y = sin\sqrt{x^2+z^2}$$
$$y = sin\sqrt{x^2+z^2}$$
 $$y = sin(x)cos(z) + cos(x)sin(z) - 2sin(z)$$
$$y = sin(x)cos(z) + cos(x)sin(z) - 2sin(z)$$
 $$y = {xz \over e^{x^2+z^2}}$$
$$y = {xz \over e^{x^2+z^2}}$$
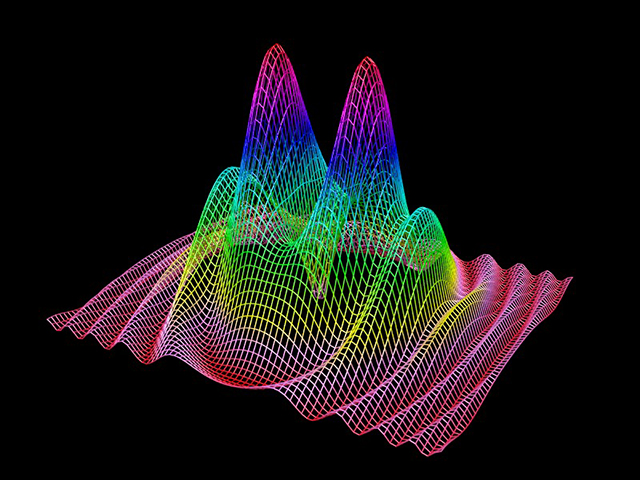 $$ y = {sin(x^2+3*z^2)\over(0.10+r) }+\frac{1}{2}(x^2+5z^2)e^{1-r} $$
$$ y = {sin(x^2+3*z^2)\over(0.10+r) }+\frac{1}{2}(x^2+5z^2)e^{1-r} $$