Le problème d'Apollonius : Comment construire un cercle tangent à trois cercles.

Il s'agit du dixième problème d'Apollonius. Il a été résolu par François Viète en s'appuyant sur la résolution des cas précédents. Il avait habilement utilisé les méthodes classiques de la géométrie euclidienne. Les constructions modernes recourent plutôt à la géométrie des inversions ou à la géométrie analytique.


Ce problème a été présenté par Pappus comme étant le dixième et le plus difficile du Traité des contacts, un des ouvrages perdus d'Apollonius. En effet, il faudra attendre 1600 pour sa résolution par François Viète qui montrera qu'il admet au maximum huit solutions. Il va résoudre les dix problèmes dans l'Apollonius Gallus.



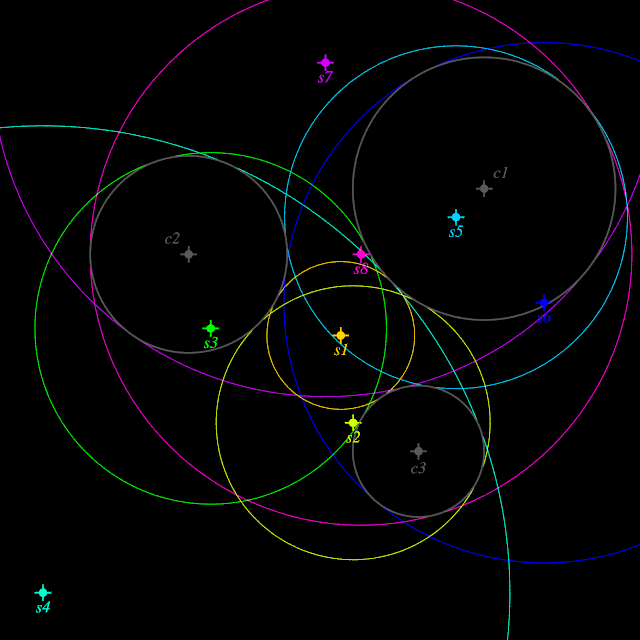
Les trois cercles donnés sont représentés en gris et leurs centres respectifs sont { c1, c2, c3 }. Les 8 cercles solutions sont représentés en couleurs avec leurs centres de { s1 ... s8 }.



Remarque sur le code source : Le tableau Signs[][] permet de définir de quelle manière les cercles sont tangents. Le -1 indique que le cercle est en dehors du cercle considéré. Le +1, l'inverse, le cercle est à l'intérieur. Si l'on prend la première ligne, tous les coefficients sont à -1. Ce qui veut dire que le cercle solution (cercle tangent aux trois autres) sera à l'extérieur des trois autres. Le cercle solution s1 et bien à l'extérieur des cercles de base. Mais ceci suppose que l'on connaît "a priori" le nombre de solutions.



Références :

• Wolfram MathWorld : Apollonius' Problem
• Problème des contacts
• CCC: Les huit solutions