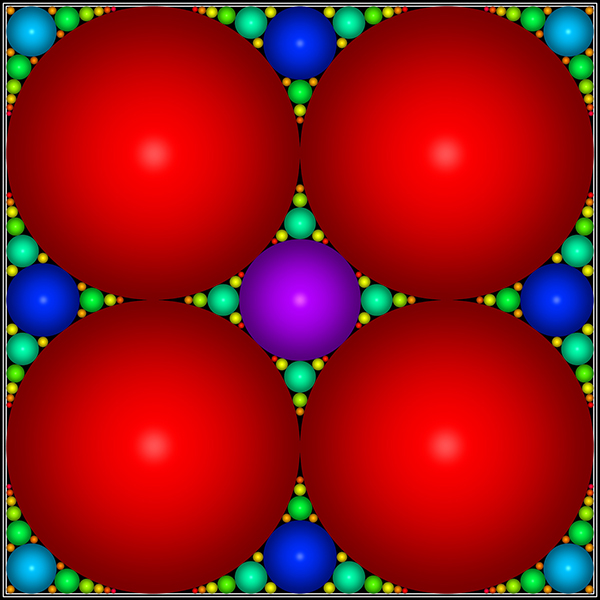
Empilements Apolloniens dans un carré.
Selon WIKIPEDIA, la figure des cercles d'Apollonius est un empilement compact de cercles dans un cercle. On procède par itérations successives en cherchant à chaque étape, un cercle tangent à d'autres cercles. Ici, l'empilement est dans un polygone (carré). On peut donc avoir à chercher des cercles tangents à des droites. Le rayon des cercles sont de plus en plus petits. Ce processus peut se répéter à l'infini. On obtient alors une figure fractale.Les quatre cas pouvant être rencontrés sont les suivants :
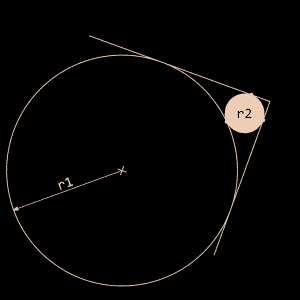
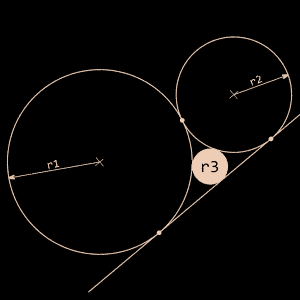
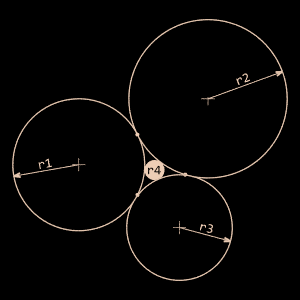
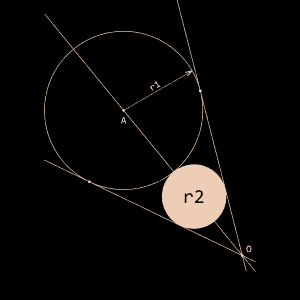
Bien que le cas numéro 1 ne soit qu'un cas particulier du cas numéro 4, il sera utilisé plusieurs fois car ici, l'empilement se fait dans un carré. Le calcul du rayon dans chaque cas ne pose pas de problème particulier : il suffit d'utiliser les théorèmes d'Apollonius, de Descartes et de Soddy (ps : non, ce ne sont pas des pseudos d'influenceurs sur les réseaux sociaux). Seul le dernier cas nécessite la norme du vecteur OA.
Détail de la construction :
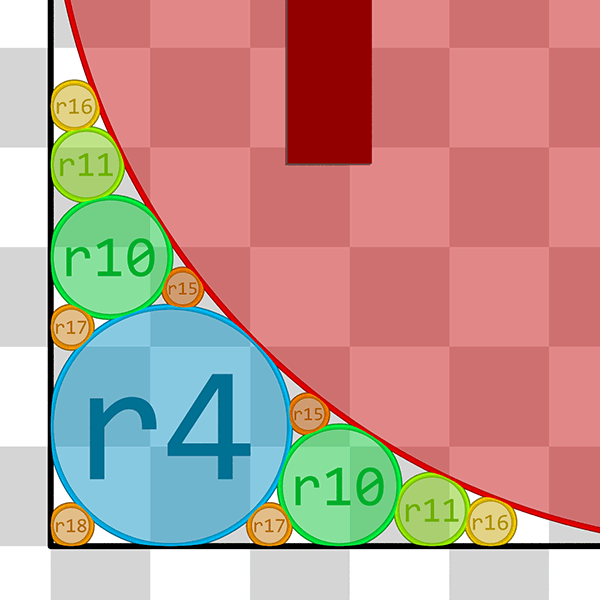
A ce stade, il y a encore de la place pour d'autres cercles ...
La représentation des cercles en utilisant l'objet cylinder{} peut être remplacée par d'objet sphere{} de manière très simple.
Dans l'image ci-dessous, les couleurs sont fonction du rayon de chaque cercle sur une échelle logarithmique en base 7.