Chapiter 2 : Transformation des solides
POVRay nous offre plusieurs opérations permant de transformer les solides : la mise à l'échelle scale, les déplacements linéaires translate et les rotations rotate.Dans les exemples ci-dessous, nous utiliserons deux solides, un cube et une sphère.

le cube est défini par les deux points :
- <0.00, 0.00, 0.00>
- <-1.00, +1.00, +1.00>

la sphère définie par :
- son centre <0.00, 0.00, 0.00>
- son rayon 1.00
L'opérarateur scale permet de modifier les dimensions du solide. La syntaxe est la suivante : scale <echX, echY, echZ>. Chaque point du solide est multiplié par la valeur du vecteur. Nous avons appliqué aux deux solides ci dessous l'opérateur : scale <1.5, 0.8, 0.4>


< 0.00, 0.00, 0.00> * <1.5, 0.8, 0.4> = < 0.00, 0.00, 0.00> <-1.00, 1.00, 1.00> * <1.5, 0.8, 0.4> = <-1.50, 0.80, 0.40>Et pour la sphère :
<-1.00, -1.00, -1.00> * <1.5, 0.8, 0.4> = <-1.50, -0.80, -0.40> < 1.00, 1.00, 1.00> * <1.5, 0.8, 0.4> = < 1.50, 0.80, 0.40>
2.2 Les translations.
L'opérateur translate permet de déplacer un solide. La syntaxe est la suivante : translate <distanceX, distanceY, distanceZ>. L'opérateur translate attend toujours un vecteur comme argument. Ceci peut conduire à des résultats inattendus car translate 3 par exemple, va déplacer l'objet de 3 unités dans chaque direction. POVRay interprète cette commande comme translate <3, 3, 3>. Il faut donc toujours spécificier les valeurs de translation pour chacun des axes.
POVRay offre bien sur des facilités dans ce cas avec des vecteurs prédéfinis x, y et z. Ces vecteurs sont déclarés comme suit : x = <1, 0, 0> y = <0, 1, 0> z = <0, 0, 1>.
Nous pouvons donc utiliser translate 2.75*y pour déplacer le solide de 2.75 unités suivant l'axe y car POVRay interprètera cette commande comme : 2.75*<0, 1, 0> = <0, 2.75, 0>.
2.3 Les rotations.
L'opérarateur rotate applique une rotation à un objet par rapport à l'origine. La syntaxe est la suivante : rotate <angleX, angleY, angleZ>. Les angles ont exprimés en dégrés. L'opérateur rotate attend lui aussi une vecteur comme argument. Les remarques faites pour translate sont donc aussi valables pour rotate.
Nous pouvons donc écrire rotate <30, -45, 75> pour faire tourner un solide de 30° autour de l'axe x, de 315° autour de l'axe y et de 75° autour de l'axe z. De la même manière, si nous voulons faire pivoter un solide de 53° autour de l'axe z, nous pouvons écrire : rotate 53*z.
Les images ci-dessous montre les rotations autour de chacun des trois axes :
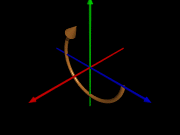
Rotation autour de x

Rotation autour de y

Rotation autour de z
Remarque : Si l'on applique une rotation à un solide qui n'est pas centré sur l'axe de rotation choisi, celui-ci décrira une orbite autour de cet axe et pas une rotation.
2.4 Orde des transformations.
Et non, l'ordre des transformations n'est pas commutatif. La remarque du paragraphe précédent est importante. Si le solide est sur l'axe de rotation, rotate applique vraiment une rotation. Si le solide n'est pas sur l'axe de rotation, rotate le mettra en orbite autour de cet axe. Les images ci-dessous illustrent l'ordre des transformations :

Position de départ
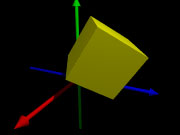
rotate PUIS translate

translate PUIS rotate
POVRay offre un opérateur transform { } qui permet de définir un ensemble de transformations puis de les appliquer d'un seul coup. Par exemple, on peut écrire :
#declare myTransforms = transform {
rotate 23*x // rotation de 23° autour de l'axe x.
scale 5 // mise à l'échelle de 5 unité dans chaque direction.
translate <2, 5, 1> // déplacement sur chaque axe.
rotate 5*z // rotation de 5° autour de l'axe z.
}
Plus tard dans la description de la scène, on pourra utiliser :
sphere {
<2, -1, 5> // centre de la sphère
1.25 // rayon de la sphère
transform { myTransforms } // applique toutes les transformations déjà définies
...
}
Les transformations ainsi définies peuvent être utilisées n'importe où et plusieurs fois dans le SDL.
2.5 Les matrices de transformation.
Les matrices de transformations offrent la possibilité d'appliquer toutes sortes de transformations physique à un solide en une seule opération. La contre partie de cette puissance est la complexité d'utilisation des matrices. Une matrice de transformation est définie dans POVRay comme suit :
matrix < ax, ay, az,
bx, by, bz,
cx, cy, cz,
dx, dy, dz >
Un point P de coordonnées <px, py, pz> sera transformé en un point Q par la matrice de cette façon :Qx = ax*Px + bx*Py + cx*Pz + dx Qy = ay*Px + by*Py + cy*Pz + dy Qz = az*Px + bz*Py + cz*Pz + dzavec :
- pour la mise à l'échelle : ax = echX, by = echY et cz = echZ.
- pour la translation : ax = 1, by = 1, cz = 1, dx = distX, dy = distY et dz = distZ.
- pour la rotation : ça se complique un tout petit peu :
- autour de l'axe x :
ax = 1, by = cosinus(angleX), bz = sinus(angleX), cy = -sinus(angleX), cz = cosinus(angleX) - autour de l'axe y :
ax = cosinus(angleY), az = -sinus(angleY), by = 1, cx = sinus(angleY), cz = cos(angleY). - autour de l'axe z :
ax = cosinus(angleZ), ay = sinus(angleZ), bx = -sinus(angleZ), by = cosinus(angleZ), cz = 1. - les autres valeurs étant à zéro.
- autour de l'axe x :