GALERIE     EN COURS     SCENES     MACROS     GUIDE     PORTFOLIO     A PROPOS


L'objet lathe
Un lathe est un objet obtenu en faisant tourner un profil autour de l'axe y. C'est exactement ce que fait un tour de mécanicien ou de menuisier. Pendant longtemps, j'ai négligé cet l'objet car il est difficile à maitriser. Pour définir comment les points du profil sont raccordés entre eux, il y a plusieurs methodes : linear_spline, quadratic_spline, cubic_spline, et bezier_spline.

Avec la méthode linear_spline les points sont raccordés par des droites. La facilité avec laquelle ont peut utiliser cette méthode a pour contre partie la pauvreté de l'objet généré.

Les 3 autres méthodes sont beaucoup plus riches et permettent de faire des objets plus "lissés"... mais au détriment de la complexité car il devient difficile de prévoir par quels point la courbe va passer. Ces courbes étant définie soit par des équations du 3iéme et 4iéme dégres, soit par des polynomes de Bézier.

Mais que sont les "coubres de Bézier" ? Ce sont des courbes polynomiales décrites pour la premiére fois en 1972 par l'ingénieur français Pierre Bézier qui les utilisa pour concevoir par ordinateur, des voitures automobiles. Les plus importantes courbes de Bézier, sont les cubiques, qui sont utilisées en informatique pour le graphisme et dans de multiples systémes de traitement d'image tels que PostScript, pour dessiner des courbes lissées joignant des points ou des polygones de Bézier. Les polices de caractéres TrueType™ et Type1 utilisent des courbes de Bézier quadratiques plus simples.
courbes de bezier Quatre points A, B, C et D dans le plan ou dans l'espace à trois dimensions définissent une courbe de Bézier cubique. La courbe se trace en partant du point A, en se dirigeant vers B et en arrivant au point D avec la direction CD.

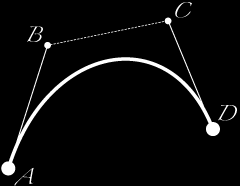
En général, la courbe ne passe ni par B ni par C; ces points sont simplement la pour donner une information de direction. La distance entre A et B détermine la longueur du déplacement dans la direction de B avant de tourner vers D.

La courbe est obligatoirement contenue dans le quadrilatére ABCD.

Les doites AB et DC sont respectivement les tangentes aux points A et D. Le déplacement des points B et C font varier la courbure en ces points qui eux, sont fixes.

Quel rapport avec le bezier_spline de POVRay ? Et puis, c'est encore plus compliqué de définir un profil avec courbes polynomiales non ?

Oui car manipuler des équation comme \( P(t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1}+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3} \) n'est pas évident, mais, car il y a un mais, depuis longtemps il existe des logiciels vectoriel qui utilisent ces courbes de Bézier avec un facilité déconcertantes ! Il s'agit (liste non limitative) de logiciels comme Abobe™ Illustrator et Macromedia™ FreeHand (qui malheureusement n'existe plus et qui a été lachement assassiné par Adobe) pour les plus connus. Ces logiciels utilisent comme langage Postscript™. Vous pouvez aller sur la page Abobe pour plus de précisions sur ce langage.

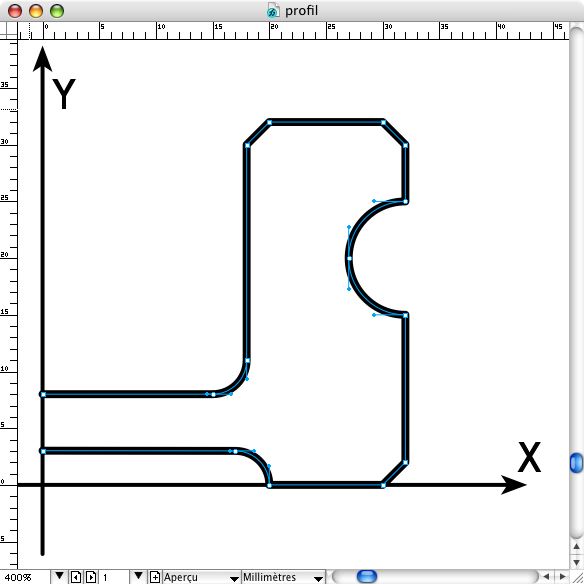
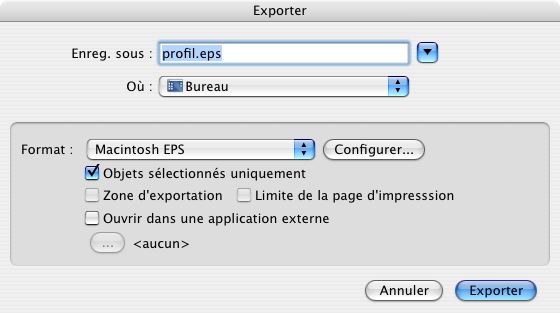
Le lien avec POVRay se précise peu à peu : on utilise un logiciel vectoriel pour tracer une courbe, on l'enregistre au format PostScript(.eps). Il ne reste "plus" qu'à extraire de ce fichier eps les données et de les mettres en forme pour en faire un lathe { } utilisant les bezier_spline. POVRay demande un ensemble de quatres points pour définir chaque segment. Ces segments de la courbe sont définis comme suit :
  • les points A et D sont les extrémités.
  • les points B et C les points de controle.
  • la tangente au point A est le segment de droite entre les points A et B.
  • la tangente au point D est la droite entre C et D.
On utilise autant de segments de quatre points qu'on le souhaite. Pour que la courbe soit continue, on doit joindre les segments en vérifiant que la relation \( point(i) = point(i-1) \) soit vraie. La courbe entiére est toujours définie par un multiple de quatre points. Chaque point étant un couple < x , y > .

Nous voiçi donc avec un fichier postscript qui contient notre courbe de Bézier, Pierre Bézier. Il faut maintenant trouver un langage pratique qui permette d'extraire facilement et de rapporter des données... qui peut se tranduire en anglais par : Pratical Extraction and Report Language... PERL ! Ce langage a de plus l'énorme avantage d'être implémenté sur quasiment toutes les plateformes informatiques existantes.

J'ai donc écrit un script PERL qui fait tout le boulot. Cool..! Enfin presque. N'ayant JAMAIS écris de PERL il a fallut que je me documente et je tiens içi à remercier les personnes qui m'ont aidées sur le forum fr.comp.lang.perl.

Le script est utilisé de la maniére suivante : eps2pov file_name [deltaX].
  • eps2pov : nom de la commande perl.
  • file_name : nom du fichier eps.
  • deltaX : nombre décimal optionnel. voir les explications plus loin.
Le script génére un fichier file_name.inc qui contient le lathe { }. Nous allons voir maintenant un exemple complet de l'utilisation de cette commande.
fenetre freehand du profil
Cet exemple fait avec Macromedia FreeHand montre un profil tracé avec l'outil "plume". Le tracé est composé de droites et de courbes. Aux point de courbures, vous pouvez voir les "balanciers", tangentes en ces points qui définissent les courbures. L'affichage dans cette fenêtre des régles, en millimétres, vous permet de définir précisement votre profil. Le lathe { } généré aura comme dimensions : 1mm égale 1 Unité POV. Le profil étant dessiné, il faut le sélectionner car lui seul est intéressant. Choisir la commande "Exporter..." du menu fichier. Le dialogue ci-dessous apparaît :
dialogue exporter de freehand
Donner un nom à votre fichier. Choisisser le format EPS. Veiller bien à ce que seul l'objet sélectionné soit exporté. Nous avons donc maintenant un fichier profil.eps. Dans une fenêtre "Terminal", aller dans le dossier ou se trouve enregistrer le fichier profil.eps par la commande cd, puis lancer le script eps2pov profil.eps. Dans le même dossier vous trouvez un fichier profil.inc qui doit contenir :
#declare profilLathe = lathe {
  bezier_spline
  56,
  <  0.000,  0.000>,<  0.000,  0.000>,< 16.567, -0.016>,< 16.997, -0.016>,
  < 16.997, -0.016>,< 18.654, -0.016>,< 19.997, -1.359>,< 19.997, -3.016>,
  < 19.997, -3.016>,< 19.997, -3.016>,< 29.997, -3.016>,< 29.997, -3.016>,
  < 29.997, -3.016>,< 29.997, -3.016>,< 31.997, -1.016>,< 31.997, -1.016>,
  < 31.997, -1.016>,< 31.997, -1.016>,< 31.997, 11.984>,< 31.997, 11.984>,
  < 31.997, 11.984>,< 29.236, 11.984>,< 26.997, 14.223>,< 26.997, 16.984>,
  < 26.997, 16.984>,< 26.997, 19.746>,< 29.236, 21.984>,< 31.997, 21.984>,
  < 31.997, 21.984>,< 31.997, 21.984>,< 31.997, 26.984>,< 31.997, 26.984>,
  < 31.997, 26.984>,< 31.997, 26.984>,< 29.997, 28.984>,< 29.997, 28.984>,
  < 29.997, 28.984>,< 29.997, 28.984>,< 19.997, 28.984>,< 19.997, 28.984>,
  < 19.997, 28.984>,< 19.997, 28.984>,< 17.997, 26.984>,< 17.997, 26.984>,
  < 17.997, 26.984>,< 17.997, 26.984>,< 17.997,  7.984>,< 17.997,  7.984>,
  < 17.997,  7.984>,< 17.997,  6.327>,< 16.654,  4.984>,< 14.997,  4.984>,
  < 14.997,  4.984>,< 14.505,  4.984>,< -0.003,  4.984>,< -0.003,  4.984>
  sturm
  }
Quelques points importants à propos de cet exemple :
  • l'objet est déclaré avec le nom du fichier auquel est accolé le mot Lathe, qui donne : profilLathe.
  • cet exemple ne fonctionne (volontairement) pas !!
  • quelques valeurs x sont négatives : -0.003. POVRay n'aime pas ça dutout. C'est justement pour pallier à ce probléme que vous pouver passer un paramétre supplémentaire à la commande eps2pov, deltaX. Cette valeur est tout simplement ajoutée à toutes les valeurs x de la courbe. Une translation de la courbe est appliqué si ce paraétre est présent. Deux cas d'utilisation de deltaX : soit comme dans cet exemple, des erreurs d'arrondis générent des valeurs négatives, soit, comme le format eps ne garde pas les origines*, la courbe n'a plus de rayon.
    * : en fait, le premier point de la courbe devient l'origine. Dans notre exemple, le troisiéme point est "plus bas" que le premier, d'ou des valeurs négatives.
  • POVRay accepte ces valeurs négatives sans probléme. Mais si vous voulez conserver votre lathe { } à partir de 0, vous devrait ajouter une ligne : translate -min_extent(profilLathe).y*y.
Fort de tout ceci nous reclançons la commande suivante :
       eps2pov profil.eps 0.003

Pour obtenir :
#declare profilLathe = lathe {
  bezier_spline
  56,
  <  0.003,  0.000>,<  0.003,  0.000>,< 16.570, -0.016>,< 17.000, -0.016>,
  < 17.000, -0.016>,< 18.657, -0.016>,< 20.000, -1.359>,< 20.000, -3.016>,
  < 20.000, -3.016>,< 20.000, -3.016>,< 30.000, -3.016>,< 30.000, -3.016>,
  < 30.000, -3.016>,< 30.000, -3.016>,< 32.000, -1.016>,< 32.000, -1.016>,
  < 32.000, -1.016>,< 32.000, -1.016>,< 32.000, 11.984>,< 32.000, 11.984>,
  < 32.000, 11.984>,< 29.239, 11.984>,< 27.000, 14.223>,< 27.000, 16.984>,
  < 27.000, 16.984>,< 27.000, 19.746>,< 29.239, 21.984>,< 32.000, 21.984>,
  < 32.000, 21.984>,< 32.000, 21.984>,< 32.000, 26.984>,< 32.000, 26.984>,
  < 32.000, 26.984>,< 32.000, 26.984>,< 30.000, 28.984>,< 30.000, 28.984>,
  < 30.000, 28.984>,< 30.000, 28.984>,< 20.000, 28.984>,< 20.000, 28.984>,
  < 20.000, 28.984>,< 20.000, 28.984>,< 18.000, 26.984>,< 18.000, 26.984>,
  < 18.000, 26.984>,< 18.000, 26.984>,< 18.000,  7.984>,< 18.000,  7.984>,
  < 18.000,  7.984>,< 18.000,  6.327>,< 16.657,  4.984>,< 15.000,  4.984>,
  < 15.000,  4.984>,< 14.508,  4.984>,<  0.000,  4.984>,<  0.000,  4.984>
  sturm
  }
Aprés copier/coller du lathe { } ou #include "profil.inc" nous pouvons ajouter dans notre scéne :
object {
  profilLathe
  translate -min_extent(profilLathe).y*y
  pigment { color Green }
  finish { ambient 0.40 diffuse 0.60 phong 0.95 phong_size 25 }
  }
Pour obtenir ces images :

image du lathe complet image du lathe coupe
Quelques remarques :
  • Comme vous avez pu le voir, ce script comporte quelques problémes. C'est pourquoi il n'est pas librement téléchargeable içi mais vous pouvez me contacter par mail pour l'obtenir.
  • Mon manque d'expérience avec PERL et PostScript y sont sûrement pour beaucoup.
  • Le script est développé dans un environement Mac OSX. Il suppose donc que l'installation de PERL est faite par défaut.
  • PERL est-il installé : $ perl -v doit donner quelque chose comme ça :

    This is perl, v5.8.1-RC3 built for darwin-thread-multi-2level
    (with 1 registered patch, see perl -V for more detail)

    Copyright 1987-2003, Larry Wall

    Perl may be copied only under the terms of either the Artistic License or the
    GNU General Public License, which may be found in the Perl 5 source kit.

    Complete documentation for Perl, including FAQ lists, should be found on
    this system using `man perl' or `perldoc perl'. If you have access to the
    Internet, point your browser at http://www.perl.com/, the Perl Home Page.

  • PERL est-il dans son emplacement par défaut :  $ whereis perl doit donner : /usr/bin/perl
  • Pour que la commande s'execute de n'importe ou, il faut ajouter le chemin du script dans la variable $PATH. J'ai modifié mon fichier .profile (j'utilise bash) en ajoutant la ligne :
         export PATH=$PATH:/chemin_complet_vers_mon_script
  • L'écriture du script PERL m'a demandé environs 4 samedi aprés-midi. Il est loin d'être optimisé et fonctionne avec des fichiers eps Mac. Le probléme du <retour-à-la-ligne> m'a posé beaucoup de problémes. Je ne suis pas sûr qu'il fonctionne directement sur plateforme Unix ou windows... mais l'adpatation devrait être simple.
  • N'ayant que Freehand à ma disposition, je n'ai pas pu tester avec d'autres logiciels. La aussi, la portablité du code PostScript Encpasulé n'est pas prouvée ...
Voici deux images pour lesquelles j'ai utilisé ce script.
exemple lathe : batons

Bâtons d'énergie extra-terrestre



exemple lathe : bouchon de carafe

Bouchon de carafe en cristal